Вписанные и описанные тела. Цилиндр, описанный около призмы Цилиндр можно описать около прямой призмы если ее основание – многоугольник, вписанный в окружность

Узнать ещё

Знание — сила. Познавательная информация

Цилиндр вписан в призму

Призма описана около цилиндра, если ее основания — многоугольники, описанные около оснований цилиндра. Соответственно, цилиндр вписан в призму.

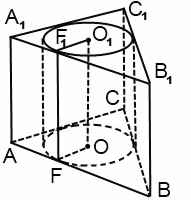
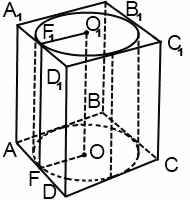
Цилиндр можно вписать в призму, если в основание призмы можно вписать окружность. Радиус вписанной окружности равен радиусу цилиндра. Высоты цилиндра и призмы равны. В школьном курсе изучается только прямой круговой цилиндр, соответственно, цилиндр в этом случае вписан в прямую призму.

Боковые грани описанной около цилиндра призмы являются касательными плоскостями к боковой поверхности цилиндра.

Найдем отношение объема призмы к объему вписанного в нее цилиндра:

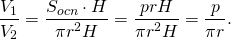
p — полупериметр основания призмы, r — радиус вписанной в основание призмы окружности и радиус цилиндра, H — высота призмы и высота цилиндра.

В частности, отношение объема правильной треугольной призмы к объему вписанного цилиндра

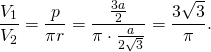
Отношение объема правильной четырехугольной призмы к объему вписанного цилиндра

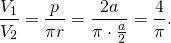
Для правильной шестиугольной призмы это отношение равно

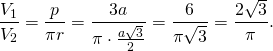
Отношение площади боковой поверхности призмы к боковой поверхности вписанного цилиндра:

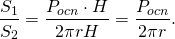
Поскольку половина периметра основания — полупериметр,

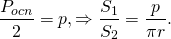
Таким образом, если цилиндр вписан в призму, отношение площади боковой поверхности призмы к боковой поверхности цилиндра равно отношению объема призмы к объему вписанного цилиндра. В частности, отношение площади боковой поверхности правильной треугольной призмы к площади боковой поверхности вписанного цилиндра

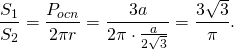
Отношение боковой поверхности правильной четырехугольной призмы к боковой поверхности вписанного цилиндра

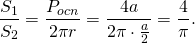
Отношение боковой поверхности правильной шестиугольной призмы к боковой поверхности вписанного цилиндра

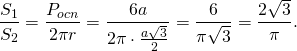
При решении задач, в которых цилиндр вписан в призму, можно рассматривать часть сечения комбинации тел плоскостью, проходящей через ось цилиндра. Для прямой призмы это сечение — прямоугольник, стороны которого равны радиусу цилиндра и высоте цилиндра. Например, AA1O1O: AA1=H, AO=r.

Вписанные и описанные тела. Цилиндр, описанный около призмы Цилиндр можно описать около прямой призмы если ее основание – многоугольник, вписанный в окружность

@ Тела вращения и многогранники могут быть вписаны одно в другое при некоторых ограничениях.

Призма называется вписанной в цилиндр , если ее основания – многоугольники, вписанные в окружности оснований цилиндра, а боковые ребра совпадают с образующими цилиндра.

В цилиндр можно вписать только такую прямую призму, основания которой можно вписать в окружность.

Призма называется описанной около цилиндра, если ее основания – многоугольники, описанные около окружностей оснований цилиндра.

Около цилиндра можно описать только такую прямую призму, основания которой – многоугольники, которые можно описать около окружности.

Очевидно, что у таких цилиндров и призм высоты равны.

Призма называется вписанной в конус, если одно ее основание вписано в окружность сечения конуса плоскостью, параллельной основанию, а другое основание принадлежит основанию конуса.

В конус можно вписать только такую прямую призму, вокруг основания которой можно описать окружность.

Очевидно, что высота вписанной призмы меньше высоты конуса.

Конус называется вписанным в прямую призму, если его вершина принадлежит одному основанию призмы, а основание конуса вписано в другое основание призмы.

Конус можно вписать только в такую призму, в основание которой можно вписать окружность.

Очевидно, что в этом случае высота конуса и высота призмы равны.

Пирамида называется вписанной в конус, если ее ребра совпадают с образующими конуса, а основание вписано в основание конуса.

Попробуйте доказать утверждение

Для того, чтобы в конус можно было вписать пирамиду, необходимо и достаточно, чтобы у нее были равные боковые ребра.

Конус называется вписанным в пирамиду, если его вершина совпадает с вершиной пирамиды, а основание вписано в основание пирамиды.

В пирамиду можно вписать конус тогда и только тогда, когда все апофемы боковых граней пирамиды равны.

Очевидно, что у таких конусов и пирамид высоты равны.

Пирамида называется вписанной в цилиндр, если ее вершина принадлежит одному основанию цилиндра, а основание вписано в другое основание цилиндра.

В цилиндр можно вписать пирамиду, основание которой можно вписать в окружность.

Очевидно, что высота вписанной пирамиды равна высоте цилиндра.

Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.

В сечении пирамиды плоскостью, параллельной основанию, получается многоугольник, подобный основанию пирамиды. Следовательно, в пирамиду можно вписать цилиндр только в том случае, если в основании пирамиды – многоугольник, в который можно вписать окружность.

Очевидно, что высота вписанного цилиндра меньше высоты пирамиды.

Многогранник называется вписанным в сферу (шар), если все его вершины лежат на сфере. Такая сфера называется описанной около многогранника.

1. Для того, чтобы около пирамиды можно было описать сферу, необходимо и достаточно, чтобы около основания пирамиды можно было описать окружность.

2. Около любой правильной пирамиды можно описать сферу.

3. Для того, чтобы около призмы можно было описать сферу, необходимо и достаточно, чтобы призма была прямая и около ее основания можно было описать окружность.

4. Около любой правильной призмы можно описать сферу.

Сфера называется вписанной в многогранник (а многогранник – описанным около сферы), если она касается всех его граней.

Полезно уметь доказывать следующие утверждения

1. В любую правильную пирамиду можно вписать сферу (шар).

2. Для того, чтобы в призму можно было вписать сферу, необходимо и достаточно, чтобы в перпендикулярное сечение призмы можно было вписать окружность и чтобы высота призмы была равна диаметру этой окружности.

3. В правильную призму можно вписать сферу тогда и только тогда, когда ее высота равна диаметру окружности, вписанной в основание.

1. Найти площадь основания правильной призмы, вписанной в цилиндр, радиус основания которого равен R .

Ответ: , где n – число сторон.

Очевидно, такой же ответ будет для правильной пирамиды, вписанной в конус.

2. В шар радиуса R вписана правильная четырехугольная пирамида с высотой, равной Н. Как связана сторона основания пирамиды с высотой пирамиды и радиусом шара?

Ответ: .

Пример 7.7.2. (КубГУ, матем., 1971 г.).

В шар радиуса R вписана правильная треугольная пирамида с плоским углом a при вершине. Найти объем пирамиды, а также боковую поверхность конуса, описанного около указанной пирамиды. Решение

DM – диаметр шара. Тогда в сечении шара, проходящем через диаметр DM и точку А, получим прямоугольный треугольник AMD . Из метрических соотношений в прямоугольном треугольнике имеем .

, откуда .

Тогда площадь основания найдем по формуле .

И из формулы находим объем пирамиды

.

Ребро AD по определению описанного конуса является его образующей. Тогда найдем боковую поверхность описанного конуса по формуле S _бок = p r1. S _бок .

Ответ: ; S _бок .

Пример 7.7.3. (КубГУ, матем., 1979 г.)

В конус, образующая которого длины наклонена к плоскости основания под углом a , вписана правильная n -угольная призма, все ребра которой имеют равные длины. Найти полную поверхность призмы. Решение

По условию все ребра n – угольной призмы равны, следовательно, ее грани – квадраты. Пусть сторона квадрата равна a, тогда S _бок , .

Задача свелась к нескольким планиметрическим соотношениям. Из прямоугольного треугольника АОК находим .

, , тогда

, тогда S _бок ,

.

S _п = S _бок + 2

.

Ответ: .

Пример 7.7.4. (КубГУ, матем., 1991 г.)

В основании пирамиды лежит квадрат со стороной а. Высота пирамиды проходит через середину одного из ребер основания и равна . Найти радиус сферы, описанной около пирамиды. Решение

В силу равноудаленности точки О от вершин S, A, B, C, D следует, что OABCD – правильная четырехугольная пирамида.

Следовательно, на грань ABCD точка О проектируется в точку М – точку пересечения диагоналей.

Следовательно, треугольник SAD – равносторонний и OASD – правильная треугольная пирамида. Тогда точка О проектируется на грань SAD в центр треугольника SAD . Отсюда , .

Из треугольника SON находим искомый радиус SO

, .

Ответ: .

Вписанные и описанные тела. Цилиндр, описанный около призмы Цилиндр можно описать около прямой призмы если ее основание – многоугольник, вписанный в окружность. – презентация

Презентация была опубликована 6 лет назад пользователемschool-gimnazia.ucoz.org

Похожие презентации

Презентация на тему: ” Вписанные и описанные тела. Цилиндр, описанный около призмы Цилиндр можно описать около прямой призмы если ее основание – многоугольник, вписанный в окружность.” — Транскрипт:

1 Вписанные и описанные тела

2 Цилиндр, описанный около призмы Цилиндр можно описать около прямой призмы если ее основание – многоугольник, вписанный в окружность. Радиус цилиндра R равен радиусу этой окружности Ось цилиндра лежит на одной прямой с высотой Н призмы, соединяющей центры окружностей, описанных около оснований призмы

3 Цилиндр, вписанный в призму Цилиндр можно вписать в прямую призму, если ее основание – многоугольник, описанный около окружности Радиус цилиндра r равен радиусу этой окружности. Ось цилиндра лежит на одной прямой с высотой Н призмы, соединяющей центры окружностей, вписанных в основания призмы

4 Конус, описанный около пирамиды Конус можно описать около пирамиды, если ее основание – многоугольник, вписанный в окружность, а вершина пирамиды проецируется в центр этой окружности Радиус конусу R равен радиусу этой окружности, а высоты Н конуса и пирамиды совпадают

5 Конус, вписанный в пирамиду вписанный в пирамиду Конус можно описать около пирамиды, если ее основание – многоугольник, описанный около окружности, а вершина пирамиды проецируется в центр этой окружности Радиус конусу r равен радиусу этой окружности, а высоты Н конуса и пирамиды совпадают

6 Шар, писанный около цилиндра Шар можно описать около любого (прямого кругового) цилиндра. Окружность оснований лежит на поверхности шара Центр шара лежит на середине высоты, проходящей через ось цилиндра

7 Радиус шара R, радиус цилиндра r и высота цилиндра Н связаны соотношением: Сечение плоскостью, проходящей через ось цилиндра (осевое сечение)

8 Шар, вписанный в цилиндр Шар можно вписать только в такой цилиндр, высота которого равна диаметру основания (такой цилиндр называется равносторонним) Шар касается оснований цилиндра в их центрах и боковой поверхности цилиндра по окружности большого круга шара параллельной основаниям цилиндра

9 Радиус шара R равен радиусу цилиндра r, а диаметр шара равен высоте цилиндра: R=r 2R=H Сечение плоскостью, проходящей через ось цилиндра (осевое сечение)

10 Шар, описанный около конуса Шар можно описать около любого конуса. Окружность основания конуса и вершина конуса лежат на поверхности шара. Центр шара лежит на оси конуса и совпадает с центром окружности, описанной около треугольника, являющегося осевым сечением конуса

11 Радиус шара R, радиус конуса r и высота конуса Н связаны соотношением: R 2 = (H-R) 2 + r 2 Это соотношение справедливо и в том случае когда HR Сечение плоскостью, проходящей через ось конуса (осевое сечение)

12 Шар, вписанный в конус Шар можно вписать в любой конус. Шар касается основания конуса в его центе и боковой поверхности конуса по окружности, лежащей в плоскости, параллельной основанию конуса. Центр шара лежит на оси конуса и совпадает с центром окружности, вписанной в треугольник, являющийся осевым сечением конуса

13 Радиус шара R, радиус конуса r и высота конуса Н связаны соотношением: Сечение плоскостью, проходящей через ось конуса (осевое сечение)

14 Шар, описанный около призмы Шар можно описать около призмы, если она прямая и ее основания являются многоугольниками, вписанными в окружность. Центр шара лежит на середине высоты призмы, соединяющей центры окружностей, описанных около оснований призмы

15 Сечение полуплоскостью, проходящей через центр шара и боковое ребро призмы. (Полуплоскость ограничена прямой, параллельной боковому ребру призмы и проходящей через центр шара) Радиус шара R, высота призмы H и радиус окружности r, описанной около основания призмы, связаны соотношением:

16 Шар, вписанный в прямую призму Шар можно вписать в прямую призму, если ее основания являются многоугольниками, описанными около окружности, а высота призмы равна диаметру этой окружности. Радиус вписанного шара равен радиусу этой окружности. Центр шара лежит на середине высоты призмы, соединяющей центры окружностей, вписанных в основания призмы

17 Сечение полуплоскостью, перпендикулярной боковой грани призмы и проходящей через высоту призмы, соединяющую центры окружностей, вписанных в основания Радиус шара R, высота призмы H и радиус окружности r, вписанной в основание призмы, связаны соотношениями :

18 Шар, описанный около правильной пирамиды Шар можно описать около любой правильной пирамиды. Центр шара лежит на прямой, содержащей высоту пирамиды и совпадает с центром окружности, описанной около равнобедренного треугольника, боковой стороной которого является боковое ребро пирамиды, а высотой – высота пирамиды. Радиус шара равен радиусу этой окружности

19 Сечение полуплоскостью, проходящей через центр шара и боковое ребро пирамиды. (Полуплоскость ограничена прямой, проходящей через высоту пирамиды) Радиус шара R, и высота пирамиды H и радиус окружности r, описанной около основания пирамиды, связаны соотношением: R 2 = (H-R) 2 + r 2 Это соотношение справедливо и в том случае когда HR В – Боковое ребро пирамиды Н – Высота пирамиды

20 Шар, вписанный в правильную пирамиду Шар можно описать около любой правильной пирамиды. Центр шара лежит на высоте пирамиды и совпадает с центром окружности, вписанной в равнобедренный треугольник, боковой стороной которого является апофема (высота боковой грани) пирамиды, а высотой – высота пирамиды. Радиус шара равен радиусу этой окружности

21 Сечение полуплоскостью, проходящей через центр шара и апофему пирамиды. (Полуплоскость ограничена прямой, проходящей через высоту пирамиды) Радиус шара R высота пирамиды H и радиус окружности r, вписанной в основание пирамиды, связаны соотношением:

Источники:

http://www.uznateshe.ru/tsilindr-vpisan-v-prizmu/
http://mschool.kubsu.ru/cdo/shabitur/kniga/geometr/7_7/7_7.htm
http://www.myshared.ru/slide/338222/